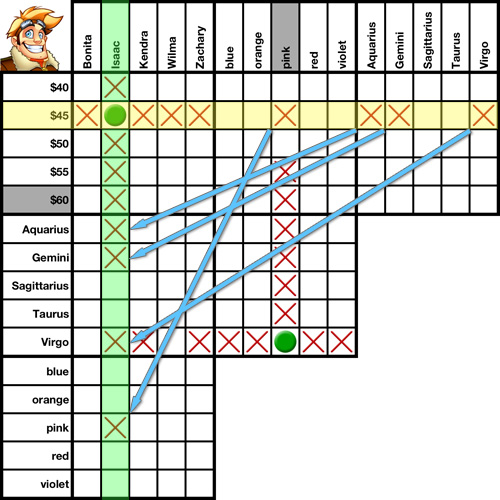
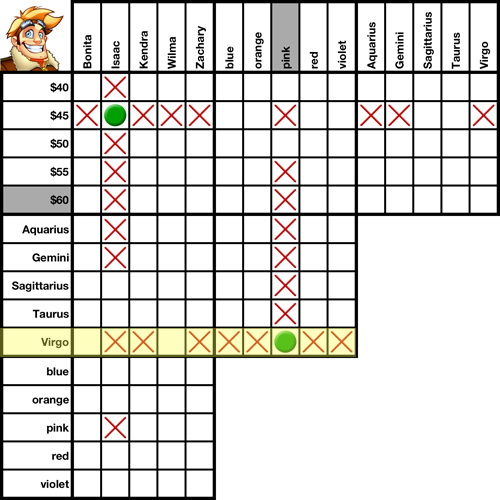
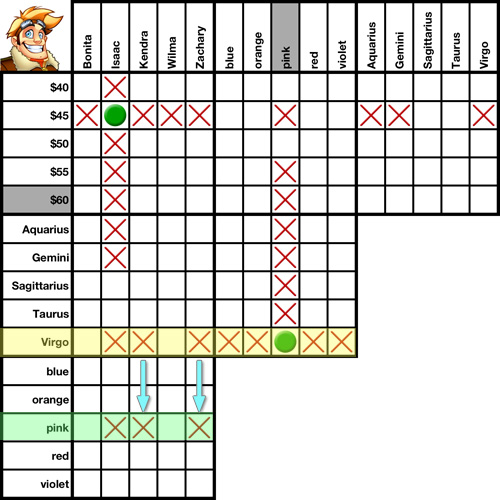
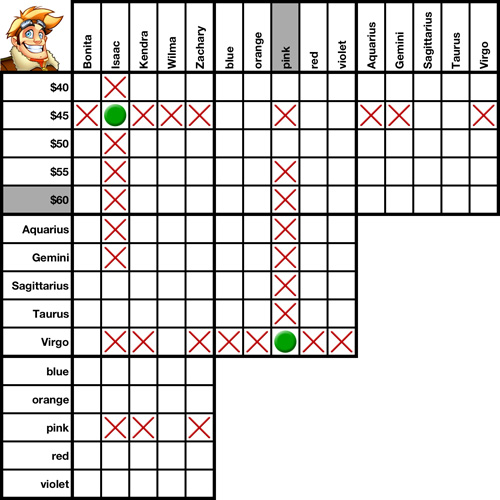
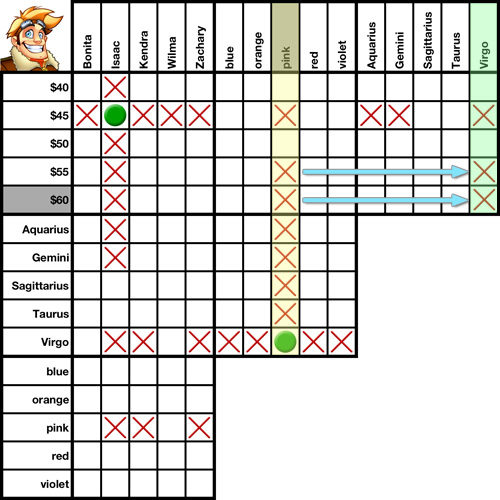
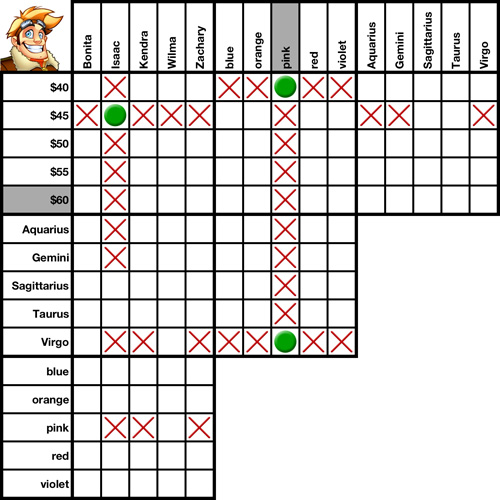
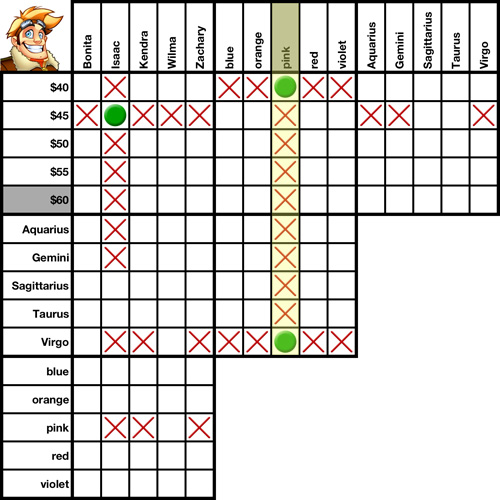
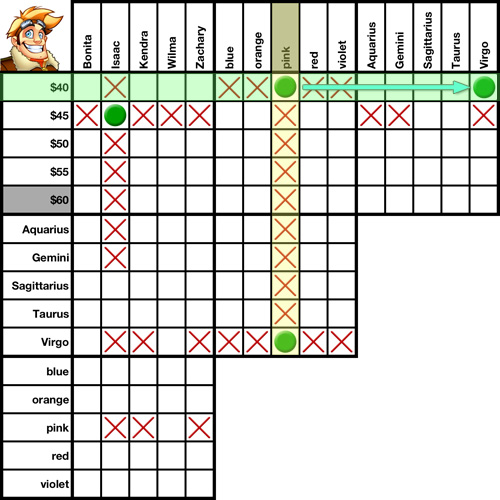
Transpositions are an essential part of solving a logic puzzle. In fact, this is without a doubt the one solving method you will use more than any other. It is a grid-only solving method, meaning you do not need to reference any clues when using it.
What is a transposition? Simply put, it's a graphical representation of one of the two most basic rules of logic:
1. If A is equal to B, and B is equal to C, then A is equal to C.
2. If A is equal to B, and B is not equal to C, then A is not equal to C.
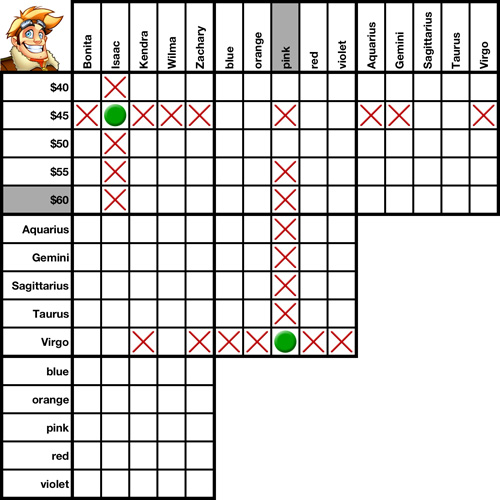
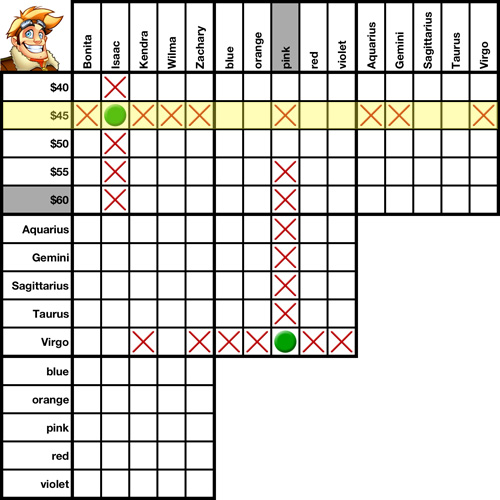
We'll use this grid to demonstrate several transpositions.