Time for another advanced method! Transitive relationships can be applied to two types of clues: (1) either/or clues or (2) unaligned pair clues.
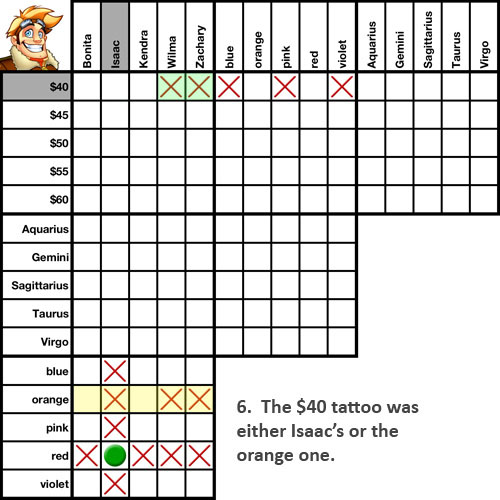
First let's see how transitive relationships work with an either/or clue. In our example we've got an either/or clue ("The $40 tattoo was either Isaac's or the orange one") and we have a true relationship already on the grid (showing Isaac's tattoo was the red one).