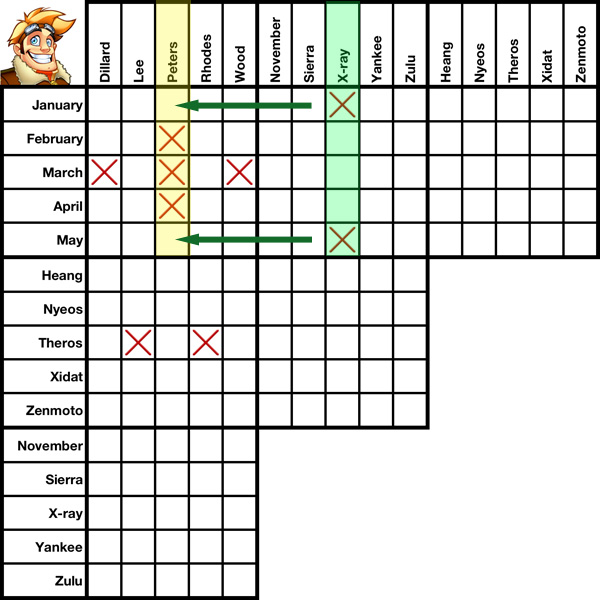
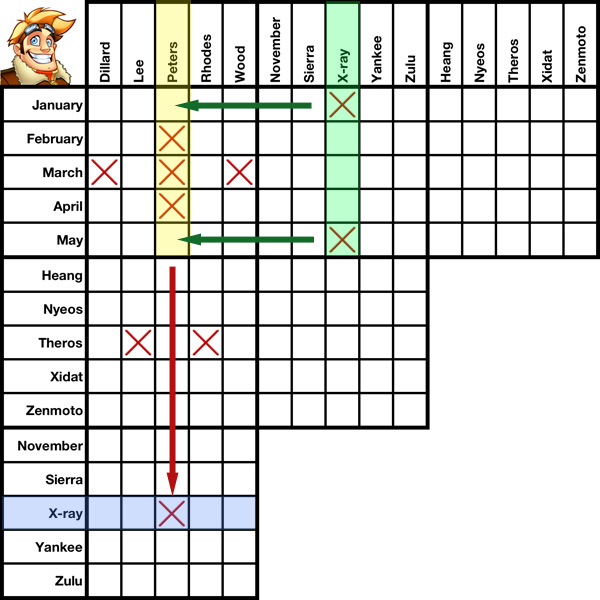
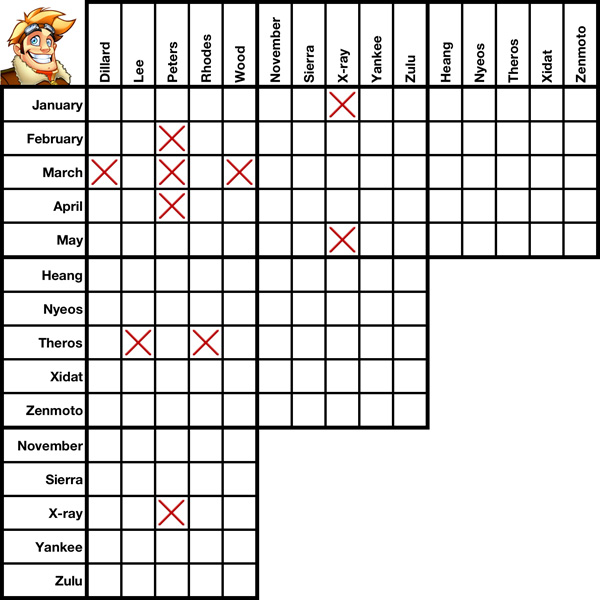
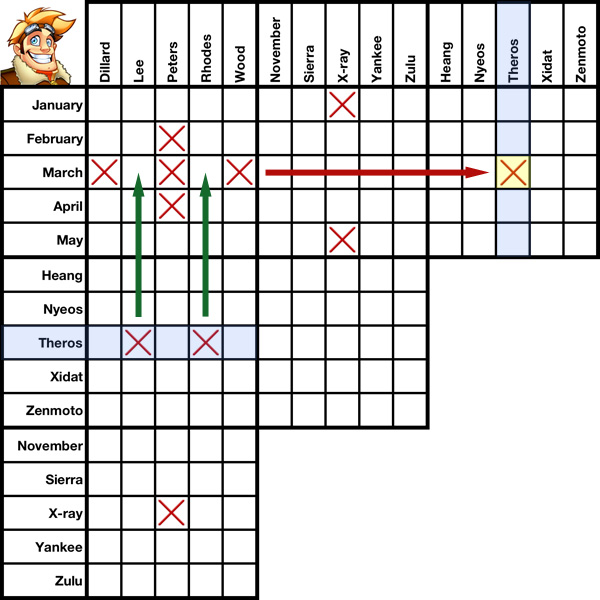
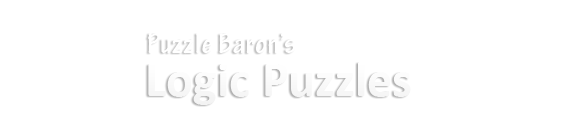Cross-elmination is an advanced solving method that comes in two flavors: geometrical and non-geometrical. It is a grid-only solving method, meaning it can be utilized without any need to refer to the clues. Although both "flavors" work in the same way and for the same reasons, geometrical cross-elimination is somewhat easier to pick out visually from a grid. Non-geometrical cross-elimination is a bit harder to spot.
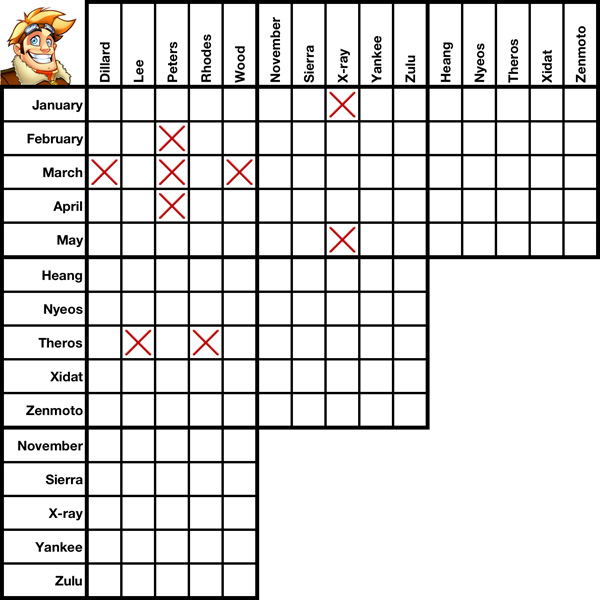
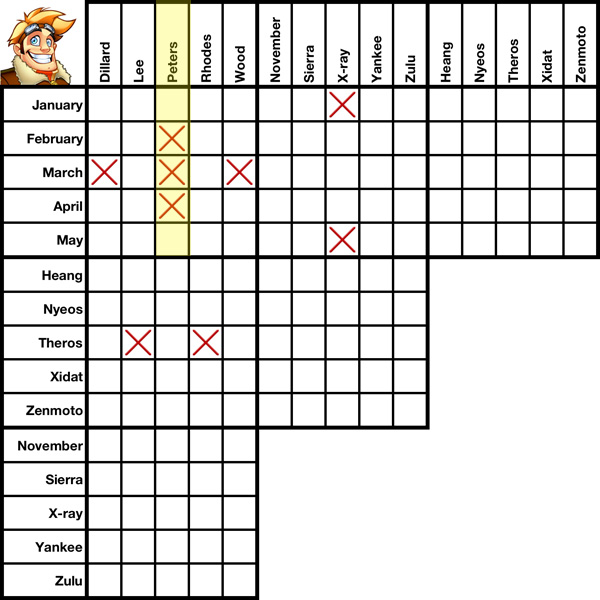
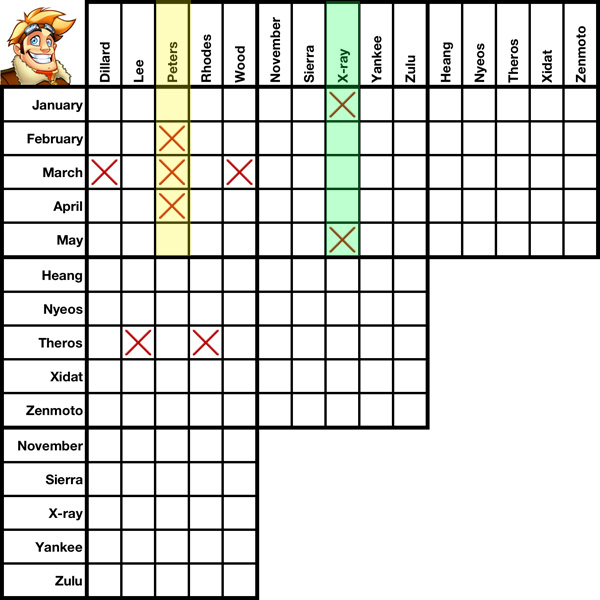
In the first five slides of this tutorial we'll discuss Geometrical Cross-Elimination using the pre-filled grid to your left. Nine boxes have been X'd out. Using nothing but geometrical cross-elimination, we'll be able to X out two more.